3 – انحراف معیار

انحراف معیار چیست؟
انحراف معیار عددی است که نشان میدهد دادهها تا چه اندازه از مقدار میانگین پراکنده هستند.
– اگر انحراف معیار کم باشد، یعنی بیشتر مقادیر به میانگین نزدیک هستند.
– اگر انحراف معیار زیاد باشد، یعنی مقادیر در محدوده وسیعتری پراکنده شدهاند.
در این آموزش از آموزشگاه برنامهنویسی و رباتیک لمپا بابل، با مفهوم انحراف معیار آشنا خواهیم شد.
مثال: در اینجا سرعت ۷ خودرو را ثبت کردهایم.
speed = [86, 87, 88, 86, 87, 85, 86]
مقدار انحراف معیار برابر است با:
0.9
یعنی بیشتر مقادیر در محدوده 0.9 واحدی از میانگین، که برابر با 86.4 است، قرار دارند. اکنون همین محاسبه را با مجموعهای از اعداد که دامنه وسیعتری دارند انجام میدهیم:
speed = [32, 111, 138, 28, 59, 77, 97]
مقدار انحراف معیار برابر است با:
37.85
یعنی بیشتر مقادیر در محدوده 37.85 واحدی از میانگین، که 77.4 است، قرار دارند. همانطور که میبینید؛ انحراف معیار نشاندهنده بزرگتر، پراکندگی بیشتر مقادیر در محدودهای وسیعتر است.
محاسبه انحراف معیار با NumPy
ماژول NumPy روشی ساده برای محاسبه انحراف معیار دارد. مثال:
import numpy
speed = [86, 87, 88, 86, 87, 85, 86]
x = numpy.std(speed)
print(x)
مثال دیگر:
import numpy
speed = [32, 111, 138, 28, 59, 77, 97]
x = numpy.std(speed)
print(x)
واریانس
واریانس عددی است که میزان پراکندگی مقادیر را نشان میدهد. در واقع، اگر جذر واریانس را بگیریم، انحراف معیار به دست میآید! و برعکس، اگر انحراف معیار را در خودش ضرب کنیم، واریانس به دست میآید.
محاسبه واریانس:
۱. ابتدا میانگین را محاسبه میکنیم:
77.4 = 7 / (32+111+138+28+59+77+97)
۲. اختلاف هر مقدار با میانگین را پیدا میکنیم:
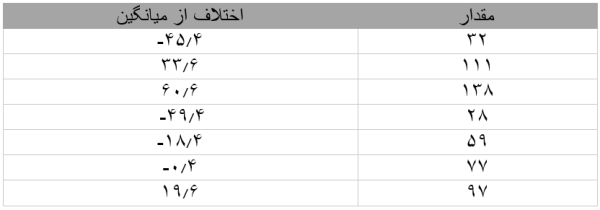
۳. مربع هر اختلاف را محاسبه میکنیم:
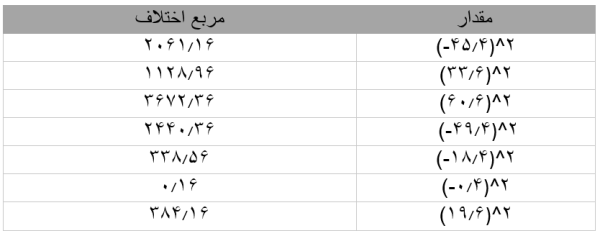
۴. واریانس را به دست میآوریم:
1432.2 = 7 / (2061.16+1128.96+3672.36+2440.36+338.56+0.16+384.16)
محاسبه واریانس با NumPy
ماژول NumPy روشی ساده برای محاسبه واریانس دارد. مثال:
import numpy
speed = [32, 111, 138, 28, 59, 77, 97]
x = numpy.var(speed)
print(x)
محاسبه انحراف معیار از واریانس
همانطور که گفتیم، انحراف معیار جذر واریانس است:
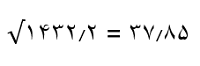
یا بهسادگی میتوان از NumPy برای محاسبه انحراف معیار استفاده کرد. مثال:
import numpy
speed = [32, 111, 138, 28, 59, 77, 97]
x = numpy.std(speed)
print(x)
نمادها
– انحراف معیار با σ (سیگما) نمایش داده میشود.
– واریانس با σ² (سیگما مربع) نمایش داده میشود.
جمعبندی
انحراف معیار و واریانس مفاهیم مهمی در یادگیری ماشین هستند، بنابراین درک آنها و نحوه محاسبهشان اهمیت دارد. در بخش های بعدی آموزش های آموزشگاه برنامه نویسی بابل، آموزشگاه لمپا، با مفاهیم دیگر یادگیری ماشین آشنا خواهیم شد.
خیلی دوره خوب و پرباریه منتطر ادامش هستیم